首页算法

# 分块

# 介绍

分块是一种思想，把一个整体划分为若干个小块，对整块整体处理，零散块单独处理。

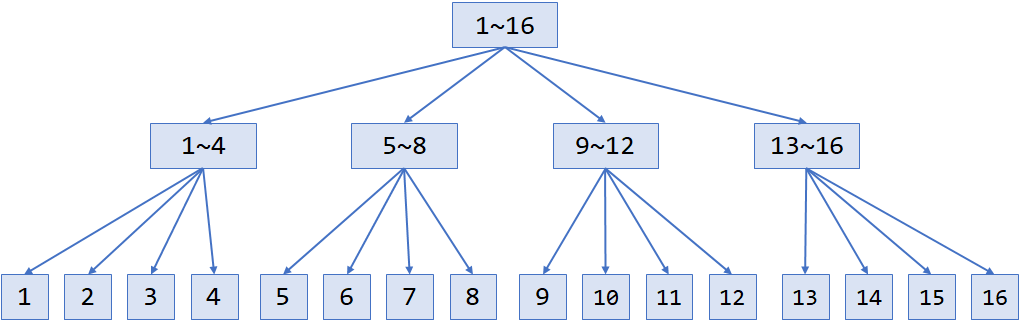
块状数组把一个长度为nn 的数组划分为aa 块，每块长度为na\frac{n}{a} 。对于一次区间操作，对区间內部的整块进行整体的操作，对区间边缘的零散块单独暴力处理。（所以分块被称为 “优雅的暴力”）

# 暴力 + 暴力 = 分块

这里，块数既不能太少也不能太多。如果太少，区间中整块的数量会很少，我们要花费大量时间处理零散块；如果太多，又会让块的长度太短，失去整体处理的意义。一般来说，我们取块数为 n\sqrt{n} ，这样在最坏情况下，我们要处理接近n\sqrt n 个整块，还要对长度为 2nn\frac{2n}{\sqrt{n}}=2n2\sqrt{n} 的零散块单独处理，总时间复杂度为O(n)O(\sqrt{n})。这是一种根号算法。

# 分块 1

image-20240110222143644

# 预处理

len = sqrt(n);// 块长
for (int i = 1; i <= n; i++) {
	cin >> a[i];
	id[i] = (i - 1) / len + 1;// 第 i 块所属的块编号
    sum[id[i]] += a[i];// 当前块的总和
    st[i] = (id[i] - 1) * len + 1;// 第 i 块所属块的开始位置
    ed[i] = min(id[i] * len, n);// 第 i 块所属块的结束位置
}

# 区间修改

void change(int l, int r, int k) {
    if (id[l] == id[r]) {// 若在同一块则直接暴力进行修改
        for (int i = l; i <= r; i++) {
            a[i] += k;
            sum[id[i]] += k;
        }
    } else {//l 与 r 不在同一块
        for (int i = l; i <= ed[l]; i++) {// 将 l 所处块暴力处理
            a[i] += k;
            sum[id[i]] += k;
        }
        for (int i = st[r]; i <= r; i++) {// 将 l 与 r 之间的块进行处理
            a[i] += k;
            sum[id[i]] += k;
        }
        for (int i = id[l] + 1; i < id[r]; i++) {// 将 r 所处块暴力处理
            add[i] += k;
        }
    }
}

# 区间查询

int query(int l, int r) {
    int ans = 0;
    if (id[l] == id[r]) {// 同一块暴力处理
        for (int i = l; i <= r; i++) {
            ans += a[i] + add[id[i]];
        }
    } else {
        for (int i = l; i <= ed[l]; i++) {// 将 l 所处块暴力处理
            ans += a[i] + add[id[i]];
        }
        for (int i = st[r]; i <= r; i++) {// 将 r 所处块暴力处理
            ans += a[i] + add[id[i]];
        }
        for (int i = ed[l] + 1; i <= st[r] - 1; i += len) {// 将 l 与 r 之间的块进行处理
            ans += sum[id[i]] + add[id[i]] * (ed[i] - st[i] + 1);
        }
    }
    return ans;
}

# 分块 2

image-20240114151905493

与第一题基本类似，但是要进行一小部分的修改，可以思考，如果我们对并不是一整个块进行乘法操作，原先块所加的值就不一样了，因此要对两边的块进行单独的操作

# 重置操作

void reset(int x) {// 将 x 所在的块进行重置
    for (int i = st[x]; i <= ed[x]; i++) {
        a[i] = (a[i] * mul[id[x]] + add[id[x]]) % m;
    }
    mul[id[x]] = 1, add[id[x]] = 0;
}

# 区间修改

void addition(int l, int r, int k) {
    if (id[l] == id[r]) {
        reset(l);// 零散块进行重置
        for (int i = l; i <= r; i++) {
            a[i] = (a[i] + k) % m;
        }
        sum[id[l]] = (sum[id[l]] + (r - l + 1) * k)%m;
    } else {
        reset(l);
        for (int i = l; i <= ed[l]; i++) {
            a[i] = (a[i] + k) % m;
        }
        sum[id[l]] = (sum[id[l]] + (ed[l] - l + 1) * k)%m;
        reset(r);
        for (int i = st[r]; i <= r; i++) {
            a[i] = (a[i] + k) % m;
        }
        sum[id[r]] = (sum[id[r]] + (r - st[r] + 1) * k)%m;
        for (int i = id[l] + 1; i < id[r]; i++) {
            add[i] = (add[i] + k) % m;
            sum[i] = (sum[i] + k * len) % m;
        }
    }
}
void multiple(int l, int r, int k) {
    if (id[l] == id[r]) {
        reset(l);
        for (int i = l; i <= r; i++) {
            sum[id[i]] = (sum[id[i]] + (k - 1) * a[i]) % m;
            a[i] = (a[i] * k) % m;
        }
    } else {
        reset(l);
        for (int i = l; i <= ed[l]; i++) {
            sum[id[i]] = (sum[id[i]] + (k - 1) * a[i]) % m;
            a[i] = (a[i] * k) % m;
        }
        reset(r);
        for (int i = st[r]; i <= r; i++) {
            sum[id[i]] = (sum[id[i]] + (k - 1) * a[i]) % m;
            a[i] = (a[i] * k) % m;
        }
        for (int i = id[l] + 1; i < id[r]; i++) {
            sum[i] = (sum[i] * k) % m;// 完整块不需要进行重置，加的数字相同，乘之后所加的数也相同
            mul[i] = (mul[i] * k) % m;
            add[i] = (add[i] * k) % m;
        }
    }
}
# 区间查询


int query(int l, int r) {
    int ans = 0;
    if (id[l] == id[r]) {
        for (int i = l; i <= r; i++) {
            ans = (ans + a[i] * mul[id[i]] + add[id[i]]) % m;
        }
    } else {
        for (int i = l; i <= ed[l]; i++) {
            ans = (ans + a[i] * mul[id[i]] + add[id[i]]) % m;
        }
        for (int i = st[r]; i <= r; i++) {
            ans = (ans + a[i] * mul[id[i]] + add[id[i]]) % m;
        }
        for (int i = ed[l] + 1; i <= st[r] - 1; i += len) {
            ans = (ans + sum[id[i]]) % m;
        }
    }
    return ans;
}
# 弹飞绵羊




# 题意：


    

  • 给定一个长度为 n 的正整数数组 a
    • 

  • m 次查询，分两种操作：
    • 

  • 查询：给定数字 i，询问从 i 开始可以执行多少次i=i+aii=i+a_i，直到i≥ni \ge n
    • 

  • 修改：给定数字 i，k (k>0)，修改ai=ka_i=k
    • 



# 思路：


我们对问题进行分块简化，对于每个块，我们只需要知道它需要跳几次才能出当前块即可，这样可以做到n\sqrt n 次就可以获取答案，


对于修改同理 **（注意题目编号从 0 开始）**


# 预处理：


void pre() {
    cin >> n;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        id[i] = (i - 1) / len + 1;
        st[i] = (id[i] - 1) * len + 1;
        ed[i] = min(id[i] * len, n);
    }
    for (int i = 1; i <= n; i = ed[i] + 1) {
        for (int j = ed[i]; j >= st[i]; j--) {
            if (j + a[j] > ed[i]) {// 这里需要从后往前推
                tar[j] = j + a[j];// 当前跳到下一块的位置
                b[j] = 1;
            } else {
                tar[j] = tar[j + a[j]];
                b[j] = b[j + a[j]] + 1;
            }
        }
    }
    cin >> m;
}
# 修改：


void change(int x, int y) {
    a[x] = y;
    for (int i = x; i >= st[x]; i--) {// 只需要从第 x 个编号向前修改即可，后面不变
        if (i + a[i] > ed[x]) {
            tar[i] = i + a[i];
            b[i] = 1;
        } else {
            tar[i] = tar[i + a[i]];
            b[i] = b[i + a[i]] + 1;
        }
    }
}
# 查询：


int query(int x) {
    int ans = 0;
    while (x <= n) {
        ans += b[x];
        x = tar[x];
    }
    return ans;
}