首页算法

# 普通莫队

# 简介

莫队算法 —— 优雅而不失复杂度的暴力

像暴力一样好写，又有分块一样时间复杂度，常数还小（不过要离线

莫队算法是由莫涛提出的算法。在莫涛提出莫队算法之前，莫队算法已经在 Codeforces 的高手圈里小范围流传，但是莫涛是第一个对莫队算法进行详细归纳总结的人。莫涛提出莫队算法时，只分析了普通莫队算法，但是经过 OIer 和 ACMer 的集体智慧改造，莫队有了多种扩展版本。

莫队算法可以解决一类离线区间询问问题，适用性极为广泛。同时将其加以扩展，便能轻松处理树上路径询问以及支持修改操作。

# 形式

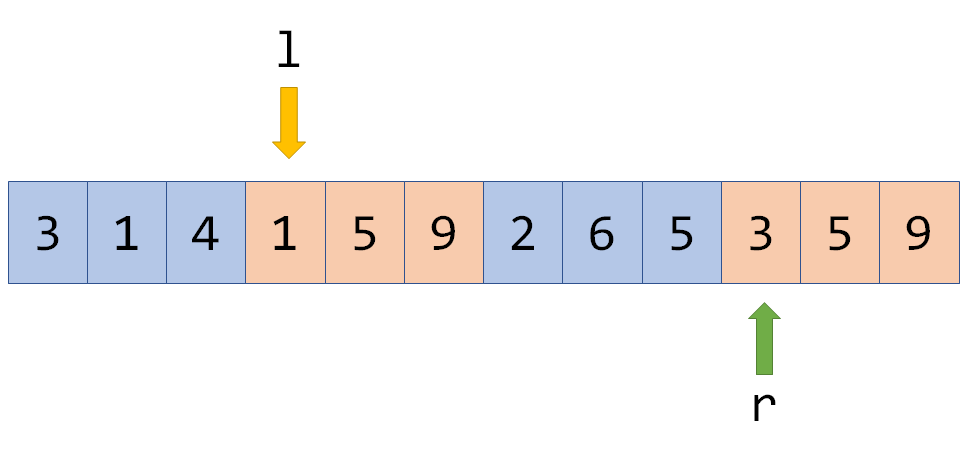
假设n=mn=m，那么对于序列上的区间询问问题，如果从[l,r][l,r] 的答案能够O(1)O(1) 扩展到[l−1,r],[l+1,r],[l,r+1],[l,r−1][l-1,r],[l+1,r],[l,r+1],[l,r-1]（即与相邻的区间) 的答案，那么可以在O(nn)O(n\sqrt{n}) 的复杂度内求出所有询问的答案。

# 解释

离线后排序，顺序处理每个询问，暴力从上一个区间的答案转移到下一个区间答案（一步一步移动即可）。

# 排序方法

对于区间[l,r][l,r], 以ll 所在块的编号为第一关键字，rr 为第二关键字从小到大排序。

# 普通莫队实现

void move(int pos, int sign) {
  // update nowAns
}
void solve() {
  BLOCK_SIZE = int(ceil(pow(n, 0.5)));
  sort(querys, querys + m);
  for (int i = 0; i < m; ++i) {
    const query &q = querys[i];
    while (l > q.l) move(--l, 1);
    while (r < q.r) move(++r, 1);
    while (l < q.l) move(l++, -1);
    while (r > q.r) move(r--, -1);
    ans[q.id] = nowAns;
  }
}
# 复杂度分析


（了解复杂度即可，以下计算证明过程仅作了解）


以下的情况在nn 和mm 同阶的前提下讨论。


首先是分块这一步，这一步的时间复杂度是O(n∗nlogn+nlogn)=O(nlogn)O(\sqrt{n}*\sqrt{n}log\sqrt{n}+nlogn)=O(nlogn)


接着就到了莫队算法的精髓了，下面我们用通俗易懂的初中方法来证明它的时间复杂度是 O(nn)O(n\sqrt{n})


# 证明


证：令每一块中LL 的最大值为max1,max2,max3,⋅⋅⋅,max∣n∣max_1,max_2,max_3,···,max_{|\sqrt{n}|}。


由第一次排序可知，max1≤max2≤⋅⋅⋅≤max∣n∣max_1 \le max_2 \le ··· \le max_{|\sqrt{n}|}


显然，对于每一块暴力求出第一个询问的时间复杂度为O(n)O(n)


考虑最坏的情况，在每一块中，RR 的最大值均为nn，每次修改操作均要将LL 由maxi−1max_{i-1} 修改至maximax_i 或由maximax_i 修改至maxi−1max_{i-1}


考虑RR：因为RR 在块中已经排好序，所以在同一块修改完它的时间复杂度为O(n)O(n)。对于所有块就是O(nn)O(n\sqrt{n})。


重点分析LL：因为每一次改变的时间复杂度都是O(maxi−maxi−1)O(max_i-max_{i-1}) 的，所以在同一块中的时间复杂度为O(n∗(maxi−maxi−1))O(\sqrt{n}*(max_i-max_{i-1}))


将每一块LL 的时间复杂度合在一起，可以得到


$  O(\sqrt{n}(max_1-1)+\sqrt{n}(max_2-max_1)+\sqrt{n}(max_3-mxa_2)+···+\sqrt n(max_{|\sqrt n|}-max_{|sqrt n -1|}))$


=O(n∗(max1−1+max2−max1+max3−max2+⋅⋅⋅+max∣n∣−1−max∣n∣−2+max∣n∣−max∣n∣−1))=O(\sqrt n*(max_1-1+max_2-max_1+max_3-max_2+···+max_{|\sqrt n|-1}-max_{|\sqrt n|-2}+max_{|\sqrt n|}-max_{|\sqrt n|-1}))


=O(n∗max∣n∣−1)=O(\sqrt n*max_{|\sqrt n|-1})


(裂项求和)


由于max∣n∣max_{|\sqrt n|} 最大为nn，所以LL 的总体时间复杂度最坏为O(nn)O(n\sqrt n)


综上所述，莫队算法的时间复杂度为O(nn)O(n\sqrt{n})


# 数列找不同


# 题意：


给你一个数列 {aia_i}，qq 个区间询问，询问每个区间内的每个数字是否互不相同


# 思路：


我们可以按照莫队的思路，将查询按左端点为第一关键字，右端点为第二关键字升序排序


第一个区间暴力跑出来，之后的区间答案在第一个区间的基础上进行获取


那区间的答案如何获取呢？我们使用一个 answer 变量来记录我们当前出现的数字种类，若ans=r−l+1ans=r-l+1，则说明没有出现相同数字，我们给答案标记为 Yes


# 查询的结构体


struct query {
    int l, r, id;
    bool operator<(const query &rhs) const {
        return l<rhs.r||l==rhs.l&&r<rhs.r;
    }
} q[N];
# 指针的移动


void add(int x) {
    if (++cnt[x] == 1) answer++;
}
void del(int x) {
    if (--cnt[x] == 0) answer--;
}
	while (l > q[i].l) add(a[--l]);
	while (r < q[i].r) add(a[++r]);
	while (l < q[i].l) del(a[l++]);
	while (r > q[i].r) del(a[r--]);
# 主函数


void solve() {
    cin >> n >> m;
    // len = sqrt(n);
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= m; i++) {
        cin >> q[i].l >> q[i].r;
        q[i].id = i;
    }
    sort(q + 1, q + m + 1);
    for (int i = 1, l = 1, r = 0; i <= m; i++) {
        while (l > q[i].l) add(a[--l]);
        while (r < q[i].r) add(a[++r]);
        while (l < q[i].l) del(a[l++]);
        while (r > q[i].r) del(a[r--]);
        if (answer == q[i].r - q[i].l + 1)
            ans[q[i].id] = 1;
        else
            ans[q[i].id] = 0;
    }
    for (int i = 1; i <= m; i++) cout << (ans[i] ? "Yes" : "No") << '\n';
}
然后提交就会发现image-20240117221411964


# 解决方法


我们把所有的元素分成多个块（即分块）。分了块跑的会更快。再按照右端点从小到大，左端点块编号相同按右端点从小到大。


struct query {
    int l, r, id;
    bool operator<(const query &rhs) const {  // 重载 & lt; 运算符
        if ((l - 1) / len  != (rhs.l - 1) / len) return l < rhs.l;// 不同块
        return r < rhs.r;// 同一块
    }
} q[N];
# 为什么要这么排序呢？


如果不是按照分块排序，那么一种直观的办法是按照左端点排序，再按照右端点排序。但是这样的表现不好。特别是面对精心设计的数据，这样方法表现得很差。


举个栗子，有 6 个询问如下：(1, 100), (2, 2), (3, 99), (4, 4), (5, 102), (6, 7)。


这个数据已经按照左端点排序了。用上述方法处理时，左端点会移动 6 次，右端点会移动移动 98+97+95+98+95=483 次。


其实我们稍微改变一下询问处理的顺序就能做得更好：(2, 2), (4, 4), (6, 7), (5, 102), (3, 99), (1, 100)。


左端点移动次数为 2+2+1+2+2=9 次，比原来稍多。右端点移动次数为 2+3+95+3+1=104，右端点的移动次数大大降低了。


# 上面的过程启发我们：我们不应该严格按照升序排序，而是根据需要灵活一点的排序方法


image-20240117221442778


# 小 Z 的袜子


# 题意：


有一个长度为nn 的序列 {cic_i}。现在给出mm 个数l,rl,r，从编号在ll 到rr 之间的数随机选出两个不同的数，求两个数相等的概率


# 思路：


对于区间[l,r][l,r]，以ll 所在块的编号为第一关键字，rr 为第二关键字从小到大排序。


然后从序列的第一个询问开始计算答案，第一个询问通过直接暴力算出，复杂度为O(n)O(n)，后面的询问在前一个询问的基础上得到答案。


具体做法：


对于区间[i,i][i,i]，由于区间只有一个元素，我们很容易就能知道答案。然后一步一步从当前区间（已知答案）向下一个区间靠近。


我们设colicol_i 表示当前颜色ii 出现了多少次，ansans 为当前共有多少种可行的配对方案（有多少种可以选到一双颜色相同的袜子），表示然后每次移动的时候更新答案 —— 设当前颜色为kk，如果是增长区间就是ansans 加上 $\left (\begin {matrix}   col_k + 1 \ 2 \end {matrix} \right) -  \left ( \begin {matrix}   col_k \ 2 \end {matrix} \right) $$，如果是缩短就是 ans 减去 $$\left ( \begin {matrix}   col_k \ 2 \end {matrix} \right) - \left ( \begin {matrix}   col_k-1 \ 2 \end {matrix} \right)  $ binom{col[k]}{2}-binom{col[k]-1}{2}。


而这个询问的答案就是ans(r−l+12)\frac{ans}{\left( \begin{matrix}   r-l+1 \\ 2 \end{matrix} \right) }。


这里有个优化：(a2)=a(a−1)2\left( \begin{matrix}   a \\ 2 \end{matrix} \right) = \frac{a(a-1)}{2}


所以(a+12)−(a2)=(a+1)a2−a(a−1)2=a2∗(a+1−a+1)=a2∗2=a\left( \begin{matrix}   a+1 \\ 2 \end{matrix} \right) - \left( \begin{matrix}   a \\ 2 \end{matrix} \right) = \frac{(a+1)a}{2} - \frac{a(a-1)}{2} = \frac{a}{2} * (a+1-a+1) = \frac{a}{2}*2 = a


所以(colk+12)−(colk2)=colk\left( \begin{matrix}   col_k + 1 \\ 2 \end{matrix} \right) -\left( \begin{matrix}   col_k \\ 2 \end{matrix} \right) = col_k


算法总复杂度O(nn)O(n\sqrt{n})


下面的代码中  ans2  表示答案的分母 (denominator)， ans1  表示分子 (numerator)， len  表示块的大小：qrt{n}， a  是输入的数组， query  是存储询问的结构体， q  是询问序列（排序后的)，  cnt  是当前袜子的个数


#include <bits/stdc++.h>
using namespace std;
#define int long long
#ifdef ONLINE_JUDGE
constexpr int N = 5e4 + 7;
#else
constexpr int N = 1e3 + 7;
#endif
int a[N], n, m, sum, ans1[N], len, ans2[N], cnt[N];
struct query {
    int l, r, id;
    bool operator<(const query &rhs) const {  // 重载 & lt; 运算符
        if ((l - 1) / len  != (rhs.l - 1) / len) return l < rhs.l;// 不同块
        return r < rhs.r;// 同一块
    }
} q[N];
void add(int x) {
    sum += cnt[x];
    cnt[x]++;
}
void del(int x) {
    cnt[x]--;
    sum -= cnt[x];
}
void solve() {
    cin >> n >> m;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= m; i++) {
        cin >> q[i].l >> q[i].r;
        q[i].id = i;
    }
    sort(q + 1, q + m + 1);
    for (int i = 1, l = 1, r = 0; i <= m; i++) {
        if (q[i].l == q[i].r) {
            ans1[q[i].id] = 0;
            ans2[q[i].id] = 1;
            continue;
        }
        while (l > q[i].l) add(a[--l]);// 四个循环位置非常关键
        while (r < q[i].r) add(a[++r]);
        while (l < q[i].l) del(a[l++]);
        while (r > q[i].r) del(a[r--]);
        if (sum == 0) {
            ans1[q[i].id] = 0;
            ans2[q[i].id] = 1;
            continue;
        }
        ans1[q[i].id] = sum;
        ans2[q[i].id] = (r - l + 1) * (r - l) / 2;// 这里是组合数学的知识
        int t = __gcd(ans1[q[i].id], ans2[q[i].id]);
        ans1[q[i].id] /= t;
        ans2[q[i].id] /= t;
    }
    for(int i=1;i<=m;i++){
        cout<<ans1[i]<<'/'<<ans2[i]<<'\n';
    }
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    int T = 1;
    // cin >> T;
    while (T--) {
        solve();
    }
    // system("pause");
    return 0;
}
# 普通莫队的优化


我们看下面这组数据


// 设块的大小为 2 (假设)
1 1
2 100
3 1
4 100



手动模拟一下可以发现，rr 指针的移动次数大概为 300 次，我们处理完第一个块之后，l=2,r=100l=2,r=100，此时只需要移动两次ll 指针就可以得到第四个询问的答案，但是我们却将rr 指针移动到 1 来获取第三个询问的答案，再移动到 100 获取第四个询问的答案，这样多了九十几次的指针移动。我们怎么优化这个地方呢？这里我们就要用到奇偶化排序。


什么是奇偶化排序？奇偶化排序即对于属于奇数块的询问，r 按从小到大排序，对于属于偶数块的排序，r 从大到小排序，这样我们的 r 指针在处理完这个奇数块的问题后，将在返回的途中处理偶数块的问题，再向 n 移动处理下一个奇数块的问题，优化了 r 指针的移动次数，一般情况下，这种优化能让程序快 30% 左右。


struct query {
  int l, r, id;
  bool operator<(const query &rhs) const {
    if ((l - 1) / len != (rhs.l - 1) / len) return l < rhs.l;
    // 注意下面两行不能写小于（大于）等于，否则会出错
    if (((l - 1) / len + 1) & 1) return r < rhs.r;
    return r > rhs.r;
  }
};
改完之后


image-20240117214142470


# 莫队维护数据结构


# 例如莫队维护分块，莫队维护 bitset 等等


# 作业


# 题意：


给定大小为 n 的序列，每次给定四个数字l,r,a,bl,r,a,b，查询区间[l,r][l,r] 中值在[a,b][a,b] 的元素数量和元素种类数


# 思路：


求区间内固定值域的个数，我们容易联想到分块，求区间内数字的种类数量，我们容易想到莫队，本题可以就利用莫队维护分块来做


我们对值域进行分块，利用莫队来保证每一次查询时分块的数据均为当前区间内的数据，最终复杂度O(nm+mn)O(n\sqrt m + m\sqrt n)


#include <bits/stdc++.h>
using namespace std;
#ifdef ONLINE_JUDGE
    constexpr int N = 1e5+7;
#else
    constexpr int N = 1e3+7;
#endif
int n,m,a[N],ans1[N],ans2[N],len,id[N],st[N],ed[N],cnt[N],sum1[N],sum2[N];//sum1 统计数字个数，sum2 统计数字种类
struct query{
    int l,r,a,b,id;
    bool operator<(const query &rhs)const{
        if(::id[l]!=::id[rhs.l]) return l<rhs.l;
        if((::id[l])&1) return r<rhs.r;
        return r>rhs.r;
    }
}q[N];
void add(int x){
    if(!cnt[x]) sum2[id[x]]++;//x 为数字
    cnt[x]++;
    sum1[id[x]]++;
}
void del(int x){
    cnt[x]--;
    if(!cnt[x]) sum2[id[x]]--;
    sum1[id[x]]--;
}
void getans(int l,int r,int k){
    if(id[l]==id[r]){
        for(int i=l;i<=r;i++){
            if(cnt[i])   ans1[k]+=cnt[i],ans2[k]++;// 当前区间出现过 i 这个数字
        }
    }
    else{
        for(int i=l;i<=ed[l];i++){
            if(cnt[i])   ans1[k]+=cnt[i],ans2[k]++;
        }
        for(int i=st[r];i<=r;i++){
            if(cnt[i])   ans1[k]+=cnt[i],ans2[k]++;
        }
        for(int i=id[l]+1;i<id[r];i++){// 对值域在 a，b 之间的块进行统计
            ans1[k]+=sum1[i];
            ans2[k]+=sum2[i];
        }
    }
}
void solve(){
    cin>>n>>m;
    len=sqrt(n);
    for(int i=1;i<=n;i++){
        cin>>a[i];
        id[i]=(i-1)/len+1;
        st[i]=(id[i]-1)*len+1;
        ed[i]=min(id[i]*len,n);
    }
    for(int i=1;i<=m;i++){
        cin>>q[i].l>>q[i].r>>q[i].a>>q[i].b;
        q[i].id=i;
    }
    sort(q+1,q+m+1);
    for(int i=1,l=1,r=0;i<=m;i++){
        while(l>q[i].l) add(a[--l]);
        while(r<q[i].r) add(a[++r]);
        while(l<q[i].l) del(a[l++]);
        while(r>q[i].r) del(a[r--]);
        getans(q[i].a,q[i].b,q[i].id);// 查询时我们的分块数据已经是完全的了，所以直接查询值域即可
    }
    for(int i=1;i<=m;i++) cout<<ans1[i]<<' '<<ans2[i]<<'\n';
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(NULL);cout.tie(NULL);
    int T=1;
    // cin>>T;
    while(T--){  solve();  }
    //system("pause");
    return 0;
}
# 回滚莫队


# 引入


有些题目在区间转移时，可能会出现增加或者删除无法实现的问题。在只有增加不可实现或者只有删除不可实现的时候，就可以使用回滚莫队在O(nm)O(n\sqrt m) 的时间内解决问题。回滚莫队的核心思想就是：既然只能实现一个操作，那么就只使用一个操作，剩下的交给回滚解决。


回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队。以下仅介绍只使用增加操作的回滚莫队，只使用删除操作的回滚莫队和只使用增加操作的回滚莫队只在算法实现上有一点区别。回滚莫队不可使用奇偶性优化


# 只加不减的回滚莫队


我们考虑一个区间问题，若这个问题在区间转移中，加点操作得以实现，但是删点操作无法有效的实现时，就可以使用如下的莫队算法：




1.1. 对原序列进行分块，并对询问按照如下的方式排序：以左端点所在的块升序为第一关键字，以右端点升序为第二关键字


2.2. 对于处理所有左端点在块TT 内的询问，我们先将莫队区间左端点初始化为R[T]+1R[T]+1，右端点初始化为R[T]R[T]，这是一个空区间


3.3. 对于左右端点在同一个块中的询问，我们直接暴力扫描回答即可。


4.4. 对于左右端点不在同一个块中的所有询问，由于其右端点升序，我们对右端点只做加点操作，总共最多加点nn 次


5.5. 对于左右端点不在同一个块中的所有询问，其左端点是可能乱序的，我们每一次从R[T]+1R[T]+1 的位置出发，只做加点操作，到达询问位置即可，每一个询问最多加n\sqrt n 次。回答完询问后，我们撤销本次移动左端点的所有改动，使左端点回到R[T]+1R[T]+1 的位置


6.6. 按照相同的方式处理下一块




# 只减不加的回滚莫队


和上一种典型的回滚莫队类似，我们还可以实现只有删点操作没有加点操作的回滚莫队，当然，这样的前提是我们可以正确的先将整个序列加入莫队中，那么算法流程如下：




1.1. 对原序列进行分块，并对询问按照如下的方式排序：以左端点所在的块升序为第一关键字，以右端点降序序为第二关键字


2.2. 对于处理所有左端点在块TT 内的询问，我们先将莫队区间左端点初始化为L[T]L[T]，右端点初始化为nn，这是一个大区间


3.3. 对于左右端点在同一个块中的询问，我们直接暴力扫描回答即可。


4.4. 对于左右端点不在同一个块中的所有询问，由于其右端点降序，从nn 的位置开始，我们对右端点只做删点操作，总共最多删点nn 次


5.5. 对于左右端点不在同一个块中的所有询问，其左端点是可能乱序的，我们每一次从L[T]L[T] 的位置出发，只做删点操作，到达询问位置即可，每一个询问最多加n\sqrt n 次。回答完询问后，我们撤销本次移动左端点的所有改动，使左端点回到L[T]L[T] 的位置


6.6. 按照相同的方式处理下一块




# 歴史の研究


# 题意：


给定一个长度为nn 的序列，离线询问mm 个问题，每次回答区间内元素权值乘以元素出现次数的最大值。


# 思路：


我们考虑用莫队来解决这个问题，显然，为了统计每个元素的出现次数，我们要用到桶。而加点操作就很好实现了，在桶中给元素的出现次数加一，并查看是否能够更新答案即可。但是删点操作就难以实现，当我们删去一个点时，我们难以得知新的最大值是多少，所以我们用只加不减的回滚莫队。


那么回滚莫队中提到的撤销操作具体就是指在桶中减去出现次数，而不管答案是否改变。在下一次加点的过程中，答案就得以统计了。


最终复杂度O(nm)O(n\sqrt m)


#include <bits/stdc++.h>
using namespace std;
#define int long long
#ifdef ONLINE_JUDGE
constexpr int N = 1e5 + 7;
#else
constexpr int N = 1e3 + 7;
#endif
int n, m, a[N], len, cnt1[N], cnt2[N], ans[N], st[N], ed[N], id[N], b[N], p;//cnt1 为统计数字个数的桶，cnt2 为处理暴力结果的桶，ans 为答案数组，b 为离散化后的数组，p 为离散化后的数组长度
struct query {
    int l, r, id;
    bool operator<(const query &rhs) const {
        if (::id[l] != ::id[rhs.l]) return l < rhs.l;
        return r < rhs.r;
    }
} q[N];
void add(int x, int &tmp) {
    ++cnt1[x];
    tmp = max(tmp, cnt1[x] * b[x]);
}
void del(int x) { --cnt1[x]; }
void solve() {
    cin >> n >> m;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        b[i] = a[i];
        id[i] = (i - 1) / len + 1;
        st[i] = (id[i] - 1) * len + 1;
        ed[i] = min(id[i] * len, n);
    }
    for (int i = 1; i <= m; i++) {
        cin >> q[i].l >> q[i].r;
        q[i].id = i;
    }
    sort(q + 1, q + m + 1);
    // 离散化
    sort(b + 1, b + n + 1);
    p = unique(b + 1, b + n + 1) - b - 1;
    for (int i = 1; i <= n; i++)
        a[i] = lower_bound(b + 1, b + p + 1, a[i]) - b;//a 数组现在存放的是离散化后的值
    int now = 0, last = 0, lstl = 0, tmp = 0;
    for (int i = 1, l = 1, r = 0; i <= m; i++) {
        if (id[q[i].l] == id[q[i].r]) {  // 左右区间属于同一块则进行暴力处理答案
            for (int j = q[i].l; j <= q[i].r; j++) ++cnt2[a[j]];
            for (int j = q[i].l; j <= q[i].r; j++)
                ans[q[i].id] = max(ans[q[i].id], cnt2[a[j]] * b[a[j]]);
            for (int j = q[i].l; j <= q[i].r; j++) --cnt2[a[j]];
            continue;
        }
        // 访问到了新的块，先把上一个块的答案清空
        if (id[q[i].l] != last) {           
            while (r > ed[q[i].l]) del(a[r--]);   // 右指针移至上一个区间的右端点
            while (l <= ed[q[i].l]) del(a[l++]);  // 左指针右移至下一个区间的左端点
            tmp = 0;
            last = id[q[i].l];
        }
        // 扩展右指针
        while (r < q[i].r) add(a[++r], tmp);
        lstl = l;  // 准确来说 l 才是原先的左指针
        now = tmp;  // 非常重要
        // 扩展左指针
        while (lstl > q[i].l) add(a[--lstl], now);
        ans[q[i].id] = now;
        // 回滚左指针
        while (lstl < l) del(a[lstl++]);
    }
    for (int i = 1; i <= m; i++) cout << ans[i] << '\n';
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(NULL);
    cout.tie(NULL);
    int T = 1;
    // cin>>T;
    while (T--) {
        solve();
    }
    // system("pause");
    return 0;
}
# 结语：


莫队还有许多的用处，比如树上莫队，可修改莫队等，这里不做赘述，感兴趣的同学可以在互联网去了解学习


祝大家 2024 新年快乐 ^ ^