# 动态规划

<u> 动态规划（dynamic programming）</u > 是一个重要的算法范式，它将一个问题分解为一系列更小的子问题，并通过存储子问题的解来避免重复计算，从而大幅提升时间效率。

# 概述

动态规划在查找有很多重叠子问题的情况的最优解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被保存，从简单的问题直到整个问题都被解决。因此，动态规划保存递归时的结果，因而不会在解决同样的问题时花费不必要的时间。

动态规划只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

# 适用情况

1. 最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
2. 无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3. 子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率，降低了时间复杂度。

# 爬楼梯

我们先从一个简单例题开始入手，爬楼梯

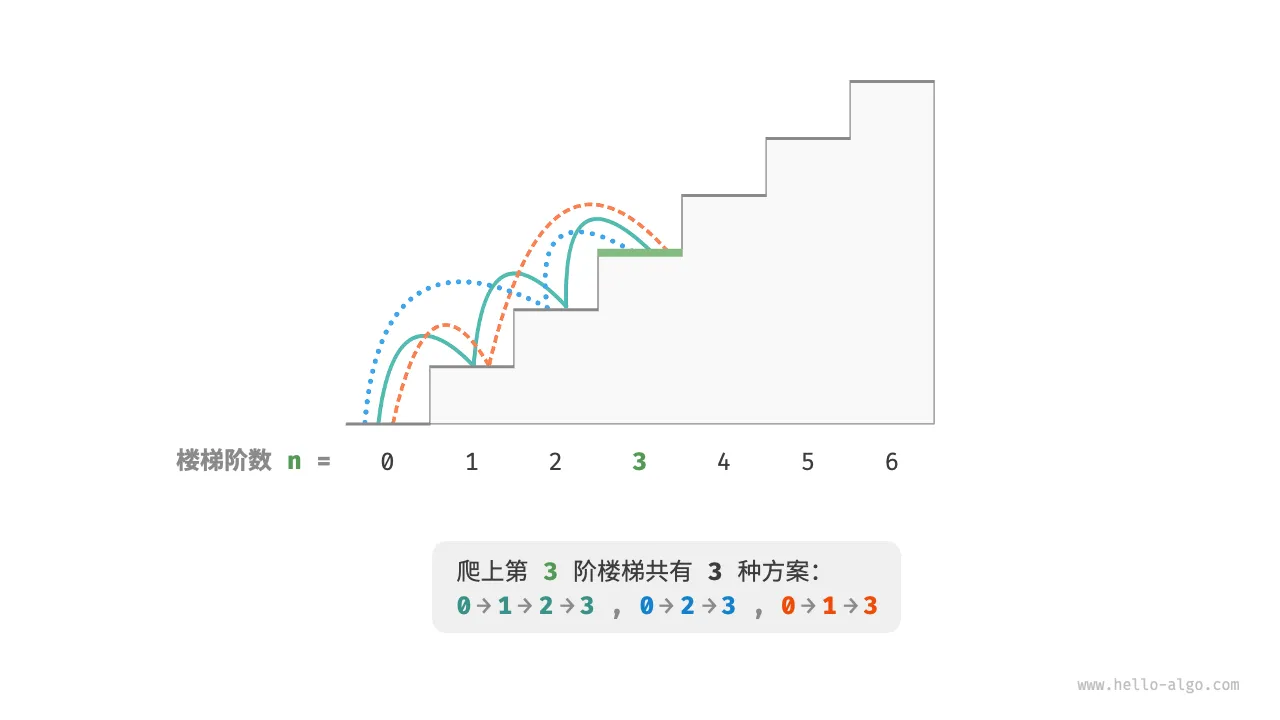
给定一个共有 n 阶的楼梯，你每步可以上 1 阶或者 2 阶，请问有多少种方案可以爬到楼顶？

如下图所示，对于一个 $3$ 阶楼梯，共有 $3$ 种方案可以爬到楼顶。

# 方法一：暴力搜索

回溯算法通常并不显式地对问题进行拆解，而是将求解问题看作一系列决策步骤，通过试探和剪枝，搜索所有可能的解。

我们可以尝试从问题分解的角度分析这道题。设爬到第 $i$ 阶共有 $dp[i]$ 种方案，那么 $dp[i]$ 就是原问题，其子问题包括：

$$dp[i-1], dp[i-2], \dots, dp[2], dp[1]$$

由于每轮只能上 $1$ 阶或 $2$ 阶，因此当我们站在第 $i$ 阶楼梯上时，上一轮只可能站在第 $i - 1$ 阶或第 $i - 2$ 阶上。换句话说，我们只能从第 $i -1$ 阶或第 $i - 2$ 阶迈向第 $i$ 阶。

由此便可得出一个重要推论：爬到第 $i - 1$ 阶的方案数加上爬到第 $i - 2$ 阶的方案数就等于爬到第 $i$ 阶的方案数。公式如下：

$$dp[i] = dp[i-1] + dp[i-2]$$

这意味着在爬楼梯问题中，各个子问题之间存在递推关系，原问题的解可以由子问题的解构建得来。下图展示了该递推关系。

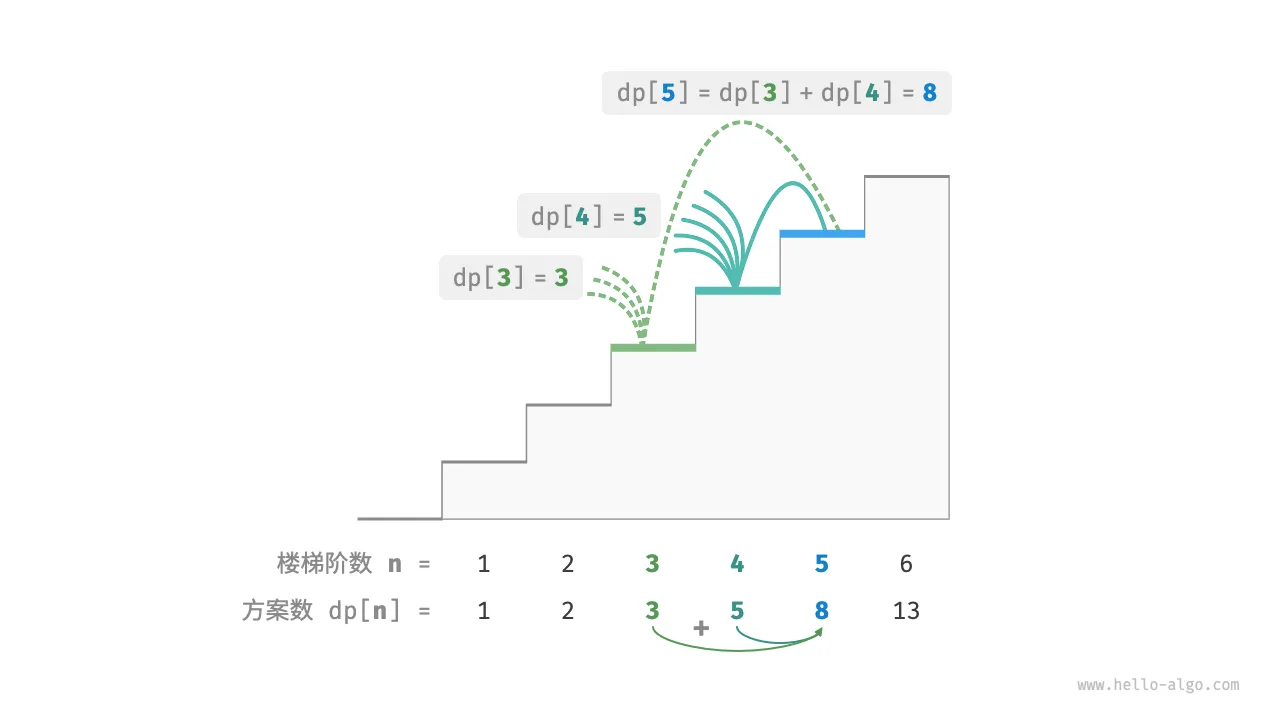
我们可以根据递推公式得到暴力搜索解法。以 $dp[n]$ 为起始点，递归地将一个较大问题拆解为两个较小问题的和，直至到达最小子问题 $dp[1]$ 和 $dp[2]$ 时返回。其中，最小子问题的解是已知的，即 $dp[1] = 1$、$dp[2] = 2$ ，表示爬到第 $1$、$2$ 阶分别有 $1$、$2$ 种方案。

如果我们用搜索来解决，那么会是怎么样一个时间复杂度呢？

/* 搜索 */

int dfs(int i) {

    // 已知 dp [1] 和 dp [2] ，返回之

    if (i == 1 || i == 2)

        return i;

    // dp[i] = dp[i-1] + dp[i-2]

    int count = dfs(i - 1) + dfs(i - 2);

    return count;

}

/* 爬楼梯：搜索 */

int climbingStairsDFS(int n) {

    return dfs(n);

}

下图展示了暴力搜索形成的递归树。对于问题 $dp[n]$ ，其递归树的深度为 $n$ ，时间复杂度为 $O(2^n)$ 。指数阶属于爆炸式增长，如果我们输入一个比较大的 $n$ ，则会陷入漫长的等待之中。

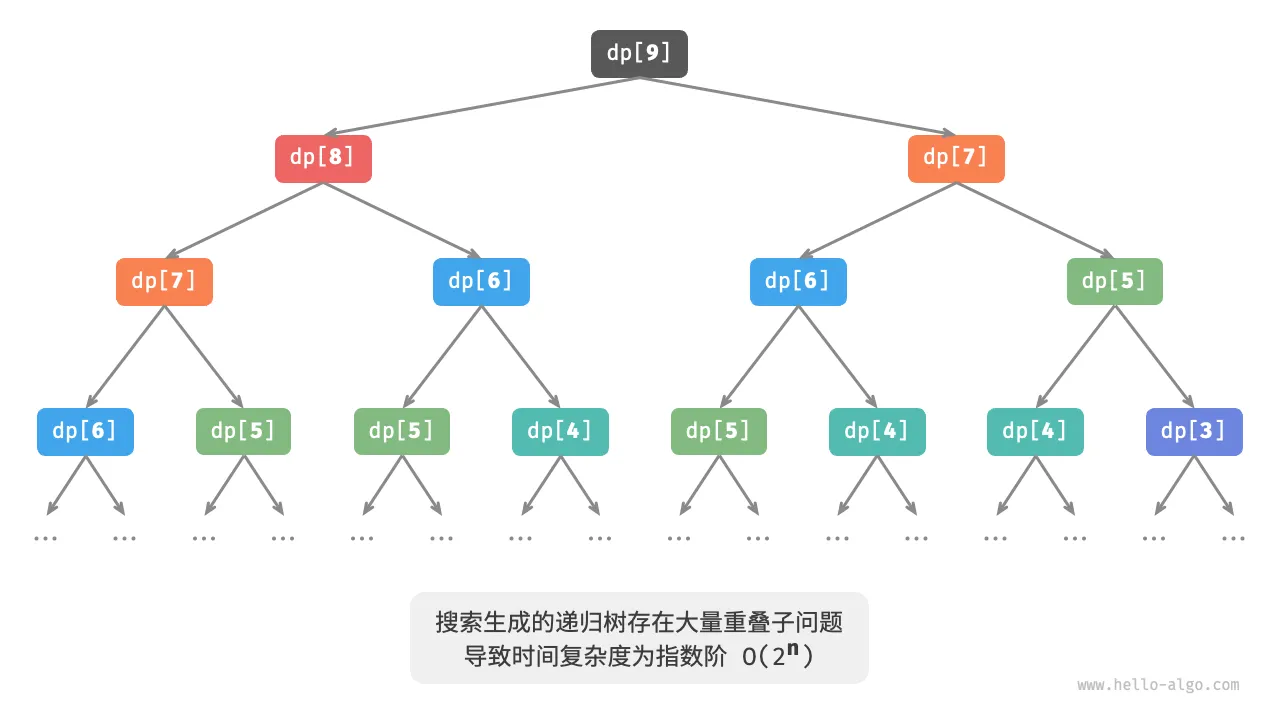
观察上图，指数阶的时间复杂度是 “重叠子问题” 导致的。例如 $dp[9]$ 被分解为 $dp[8]$ 和 $dp[7]$ ，$dp[8]$ 被分解为 $dp[7]$ 和 $dp[6]$ ，两者都包含子问题 $dp[7]$ 。

以此类推，子问题中包含更小的重叠子问题，子子孙孙无穷尽也。绝大部分计算资源都浪费在这些重叠的子问题上。

# 方法二：记忆化搜索

为了提升算法效率，我们希望所有的重叠子问题都只被计算一次。为此，我们声明一个数组 mem 来记录每个子问题的解，并在搜索过程中将重叠子问题剪枝。

1. 当首次计算 $dp[i]$ 时，我们将其记录至 mem[i] ，以便之后使用。
2. 当再次需要计算 $dp[i]$ 时，我们便可直接从 mem[i] 中获取结果，从而避免重复计算该子问题。

代码如下所示：

/* 记忆化搜索 */

int dfs(int i, vector<int> &mem) {

    // 已知 dp [1] 和 dp [2] ，返回之

    if (i == 1 || i == 2)

        return i;

    // 若存在记录 dp [i] ，则直接返回之

    if (mem[i] != -1)

        return mem[i];

    // dp[i] = dp[i-1] + dp[i-2]

    int count = dfs(i - 1, mem) + dfs(i - 2, mem);

    // 记录 dp [i]

    mem[i] = count;

    return count;

}

/* 爬楼梯：记忆化搜索 */

int climbingStairsDFSMem(int n) {

    //mem [i] 记录爬到第 i 阶的方案总数，-1 代表无记录

    vector<int> mem(n + 1, -1);

    return dfs(n, mem);

}

# 方法三：动态规划

记忆化搜索是一种 “从顶至底” 的方法：我们从原问题（根节点）开始，递归地将较大子问题分解为较小子问题，直至解已知的最小子问题（叶节点）。之后，通过回溯逐层收集子问题的解，构建出原问题的解。

与之相反，动态规划是一种 “从底至顶” 的方法：从最小子问题的解开始，迭代地构建更大子问题的解，直至得到原问题的解。

由于动态规划不包含回溯过程，因此只需使用循环迭代实现，无须使用递归。在以下代码中，我们初始化一个数组 dp 来存储子问题的解，它起到了与记忆化搜索中数组 mem 相同的记录作用：

/* 爬楼梯：动态规划 */

int climbingStairsDP(int n) {

    if (n == 1 || n == 2)

        return n;

    // 初始化 dp 表，用于存储子问题的解

    vector<int> dp(n + 1);

    // 初始状态：预设最小子问题的解

    dp[1] = 1;

    dp[2] = 2;

    // 状态转移：从较小子问题逐步求解较大子问题

    for (int i = 3; i <= n; i++) {

        dp[i] = dp[i - 1] + dp[i - 2];

    }

    return dp[n];

}

下图模拟了以上代码的执行过程。

与回溯算法一样，动态规划也使用 “状态” 概念来表示问题求解的特定阶段，每个状态都对应一个子问题以及相应的局部最优解。例如，爬楼梯问题的状态定义为当前所在楼梯阶数 $i$ 。

根据以上内容，我们可以总结出动态规划的常用术语。

• 将数组 dp 称为 <u>dp 表 </u>，$dp[i]$ 表示状态 $i$ 对应子问题的解。
• 将最小子问题对应的状态（第 $1$ 阶和第 $2$ 阶楼梯）称为 <u> 初始状态 </u>。
• 将递推公式 $dp[i] = dp[i-1] + dp[i-2]$ 称为 <u> 状态转移方程 </u>。

# 空间优化

由于 $dp[i]$ 只与 $dp[i-1]$ 和 $dp[i-2]$ 有关，因此我们无须使用一个数组 dp 来存储所有子问题的解，而只需两个变量滚动前进即可。代码如下所示：

/* 爬楼梯：空间优化后的动态规划 */

int climbingStairsDPComp(int n) {

    if (n == 1 || n == 2)

        return n;

    int a = 1, b = 2;

    for (int i = 3; i <= n; i++) {

        int tmp = b;

        b = a + b;

        a = tmp;

    }

    return b;

}

观察以上代码，由于省去了数组 dp 占用的空间，因此空间复杂度从 $O(n)$ 降至 $O(1)$ 。

在动态规划问题中，当前状态往往仅与前面有限个状态有关，这时我们可以只保留必要的状态，通过 “降维” 来节省内存空间。这种空间优化技巧被称为 “滚动变量” 或 “滚动数组”。

# 01 背包

# 题意概要：

有 $n$ 个物品和一个容量为 $W$ 的背包，每个物品有重量 $w_{i}$ 和价值 $v_{i}$ 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

在上述例题中，由于每个物体只有两种可能的状态（取与不取），对应二进制中的 $0$ 和 $1$，这类问题便被称为「0-1 背包问题」。

例题中已知条件有第 $i$ 个物品的重量 $w_{i}$，价值 $v_{i}$，以及背包的总容量 $W$。

设 DP 状态 $f_{i,j}$ 为在只能放前 $i$ 个物品的情况下，容量为 $j$ 的背包所能达到的最大总价值。

考虑转移。假设当前已经处理好了前 $i-1$ 个物品的所有状态，那么对于第 $i$ 个物品，当其不放入背包时，背包的剩余容量不变，背包中物品的总价值也不变，故这种情况的最大价值为 $f_{i-1,j}$；当其放入背包时，背包的剩余容量会减小 $w_{i}$，背包中物品的总价值会增大 $v_{i}$，故这种情况的最大价值为 $f_{i-1,j-w_{i}}+v_{i}$。

由此可以得出状态转移方程：

$$f_{i,j}=\max(f_{i-1,j},f_{i-1,j-w_{i}}+v_{i})$$

这里如果直接采用二维数组对状态进行记录，会出现 MLE。可以考虑改用滚动数组的形式来优化。

由于对 $f_i$ 有影响的只有 $f_{i-1}$，可以去掉第一维，直接用 $f_{i}$ 来表示处理到当前物品时背包容量为 $i$ 的最大价值，得出以下方程：

$$f_j=\max \left(f_j,f_{j-w_i}+v_i\right)$$

务必牢记并理解这个转移方程，因为大部分背包问题的转移方程都是在此基础上推导出来的。

for (int i = 1; i <= n; i++)

  for (int l = W; l >= w[i]; l--) f[l] = max(f[l], f[l - w[i]] + v[i]);